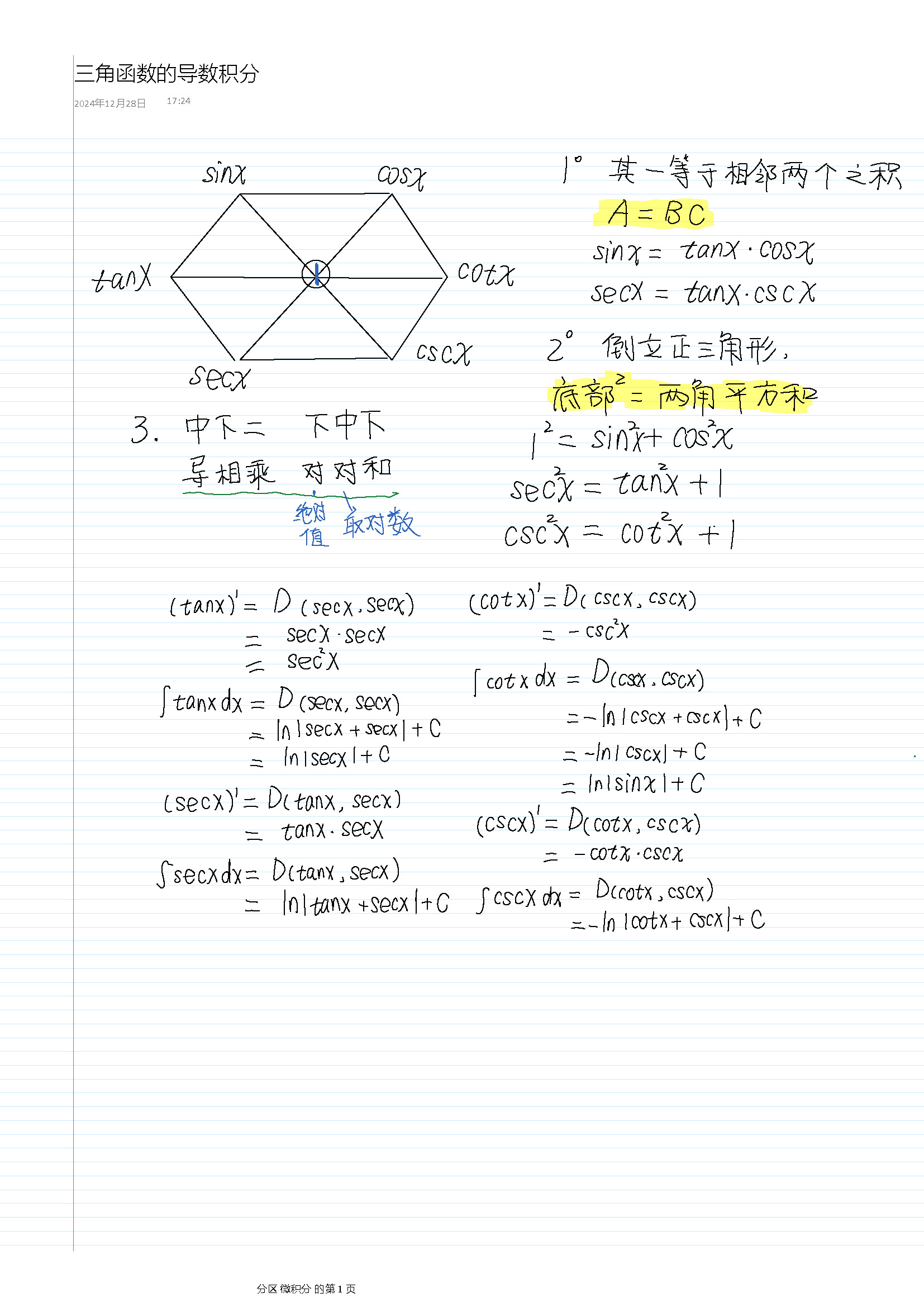
先上图
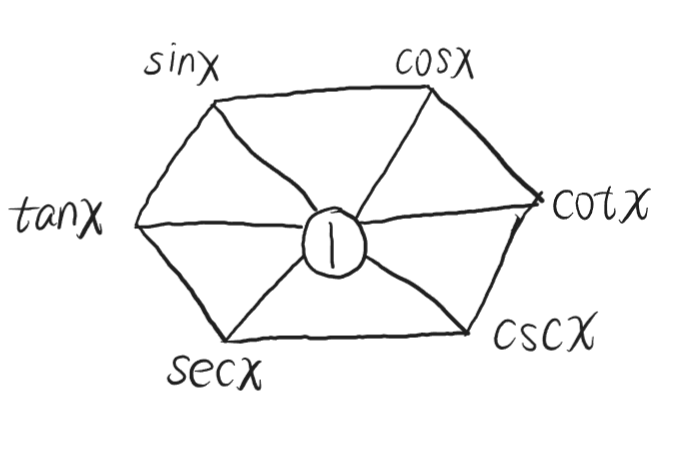
公式
b=ac
任意函数等于相邻函数的乘积
例如,
$$ \begin{aligned} \tan x & =\sec x \sin x \\ \sin x & =\tan x \cos x \\ \end{aligned} $$平方和与1的关系
我们知道,
$$ \sin^2 x + \cos^2 x = 1 $$实际上,对应图中所有的最小倒立三角形,
|
|
例如,
$$ \begin{aligned} \sin^2 x + \cos^2 x &=1 \\ \tan^2 x + 1 &= \sec^2 x \\ 1 + \cot^2 x &= \csc^2 x \end{aligned} $$求导积分
记住口诀
|
|
无论求导还是积分,中间的函数($\tan x,\cot x$)积分/求导后,只与其下方的函数有关;下方的函数求导/积分,与中间和下方(自己)有关。
如果是求导,则相乘;积分则相加,加绝对值,取对数。
例如,$\tan x$,
-
找相关函数。
$tan x$在中间,由中下二,求导/积分后与 $\sec x$,$\sec x$有关,即$D(\sec x,\sec x)$
-
确定运算符
如果是求导,则相乘:$\sec x \times \sec x$。积分,相加,加绝对值,取对数:$\ln|\sec x+\sec x|$
-
确定正负,积分加C
左边的函数求导/积分为正,右边为负。
$$\int\tan xdx=-\ln |2\sec x|+C$$ -
适当化简
如$-\ln |2\sec x|+C=-\ln |\sec x|+C$
笔记附图