先上例题
设函数$f$有二阶连续偏导,且$z=f(xy,x+y)$.
求
$$ \frac{\partial^2z}{\partial xy} $$分析
求二阶偏导,先求出一阶偏导。 当二阶偏导连续,有:
$$ \frac{\partial^2z}{\partial xy} = \frac{\partial (\frac{\partial x}{\partial y})}{\partial x} = \frac{\partial(\frac{\partial z}{\partial x})}{\partial y} $$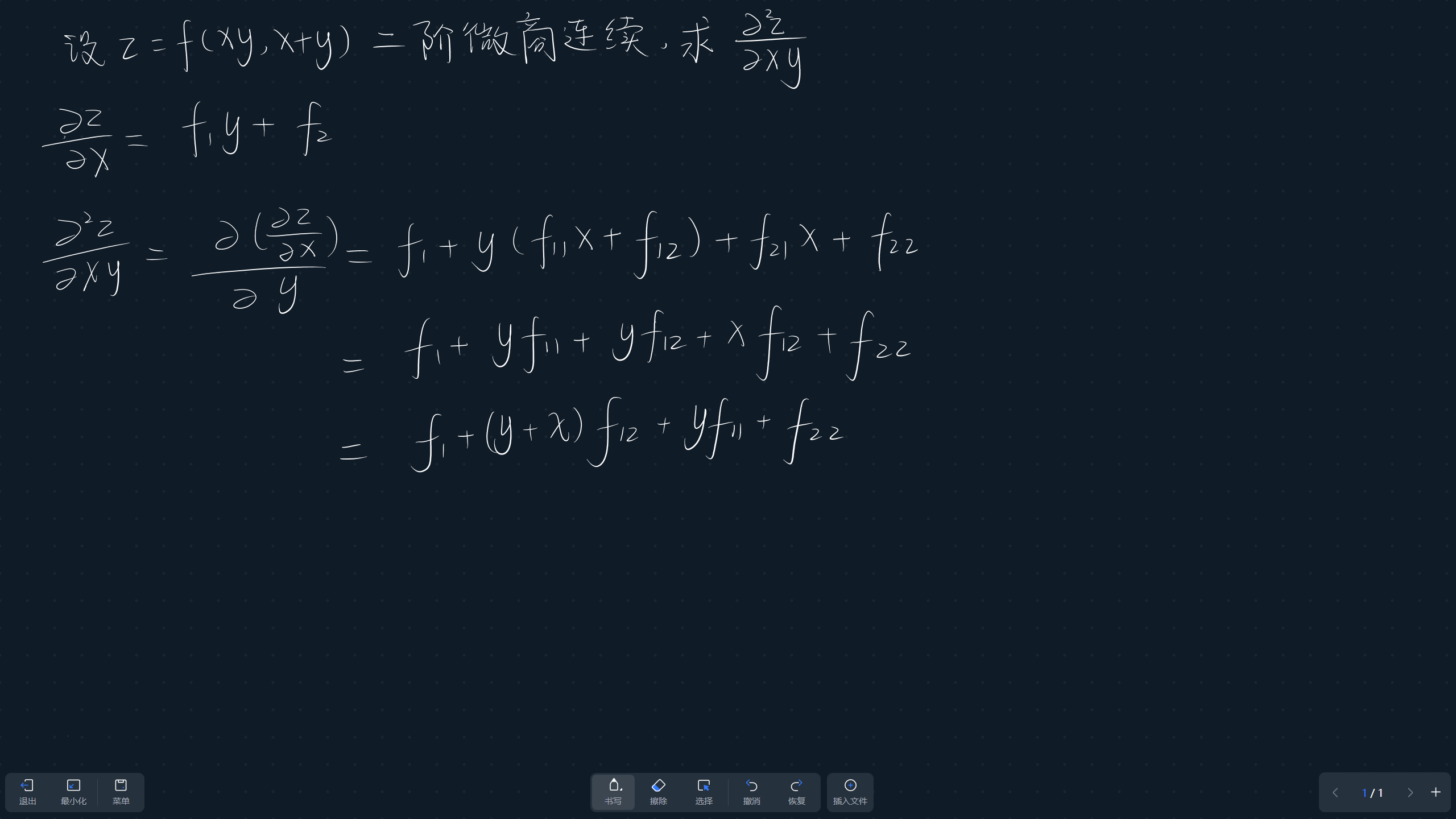
注意到$f_1$和$f_2$均有$(xy),(x+y)$的变量
总结
对于抽象函数
$$ z = f(g_1,g_2,g_3 \dots) $$其中,$g_1,g_2,g_3,\dots$是关于$x,y$的二元或一元函数
则,
$$ \begin{aligned} \frac{\partial z}{\partial x} & = f_1g_{1_x} + f_2g_{2_x} + f_3g_{3_x} +\dots \\ \frac{\partial^2z}{\partial xy} &= \frac{d(g_{1_x})}{dy}f_1+g_{1_x}(f_{11}\frac{\partial g_1}{\partial y}+f_{12}\frac{\partial g_2}{\partial y}+\dots) + \dots \end{aligned} $$注意到,$f_1$仍然是包含$g_n$的函数。例如
$$ \begin{aligned} z & = f(u,v) = u^v \\ \frac{\partial z}{\partial u} &= f_1(u,v)=vu^{v-1} \end{aligned} $$