（实验）证明列表索引操作的时间复杂度为常数阶

实验背景

时间复杂度 是为了计量算法的运行效率而提出的概念。

估测一个代码运行效率最简单的办法是记录程序的运行时间，运行时间短则效率高。但程序的运行时间往往受到计算机硬件、操作系统、编程语言和编译器等的影响。对于同一个程序，在14代Intel CPU上运行，普遍比12代 Intel CPU快；同样的代码，在Linux上可能比Windows平台快；同样的算法，用c语言实现的可能比Python实现的快；同一个c语言代码，经过clang编译可能比g++编译的更快。

因此需要一个定量的计量方法，把算法的实际运行时间抽象为理论执行步数。计算时间复杂度，最广泛使用的是 大O记法。用 $T(n)$ 来表示程序的执行步数，参数 $n$ 为问题规模。$T(n)$是关于 $n$ 函数，当 $n$ 很大时，$T(n)$ 中的很多项可以忽略不记，如

$$ T(n) = 5n^3 + 3n^2 + 2log_2n + 10000 $$

当 $n \to \infty$ 时，$3n^2$，$2log_2n$，$10000$ 在 $5n^3$ 面前显得很小，可以舍去。$n$ 的三次项的系数 $5$ 也影响不大，也可以舍去。最后就有

$$ T(n) \sim n^3 $$

因此记该算法的大$O$记法为 $O(n^3)$。

常见的大 $O$ 函数 $f(n)$ ：

$f(n)$	名称
$1$	常数
$logn$	对数
$n$	线性
$nlogn$	线性对数
$n^2$	平方
$n^3$	立方
$2^n$	指数

对于为 $O(1)$ 的程序，时间复杂度不会随问题规模 $n$ 的增大而增大，即 $T(n)=k$ 。

Python 中有一个特别的数据结构：列表。列表不同于数组，允许列表内元素有不同的数据类型。列表内的元素可以通过索引来访问，和数组的下标一样，都是从 $0$ 开始编号的。

那么Python中列表索引的具体实现算法的时间复杂度如何？索引所需要的运行时间会不会随列表的长度 $n$ 的变化而变化呢？答案是不变的。Python列表的索引并不依赖于列表的长度，列表的长度发生变化，对一次索引的时间没有影响。

我们可以通过实验来验证： Python中列表索引的时间复杂度为常数阶 。

实验原理

timeit 是Python中的一个程序运行计时模块。通过 timeit 创建一个 Timer 对象，设置要执行的语句，在通过 Timer.timeit()方法来运行，返回这条语句的运行时间。

实验代码

导入库

1
2
3


import csv
from timeit import Timer
import matplotlib.pyplot as plt

实验主体

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


def labmain(filename): # 实验主体，生成实验数据
    ls = []
    n = 10000
    endtimes = n
    fnew = open(filename,"w",newline="")
    csv_writer = csv.writer(fnew)


    for i in range(endtimes):
        ls.append(i)
        t1 = Timer(f"ls[{i}]",globals={'ls': ls})
        writerow = [i,f"{t1.timeit(number=100000):.8f}"]
        csv_writer.writerow(writerow)
    fnew.close()

t1.timeit(number=100000) 中的 number 设置执行的总次数。

数据可视化

实验主体函数将每次的运行结果写入 csv 文件，每行两个数据，一个是执行的次数序号 $n$ ，一个是程序运行时间 $y$ 。

通过 matplotlib.pyplot 可以把对应的 $x-y$ 散点图绘制出来，直观的感受 $y$ 与 $x$ 的关系。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


# 数据可视化
def plot_func(csvfile):
    fo = open(csvfile,"r")
    reader = csv.reader(fo)
    x_list = []
    y_list = []
    for row in reader:
        x_list.append(int(row[0]))
        y_list.append(float(row[1])*100)
    plt.scatter(x=x_list, y=y_list,s=3)
    plt.show()
    fo.close()

回归分析

检查 $x_i$ , $y_i$ 是否满足方程 $y=k$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


def reg_func(filename):
    fo = open(filename,"r")
    reader = csv.reader(fo)
    x_list = []
    y_list = []
    for row in reader:
        x_list.append(int(row[0]))
        y_list.append(float(row[1])*100)
    # 计算 sum_(x/y)i, sum_(x/y)i^2, sum_xi*yi
    sum_xi = sum(x_list)
    sum_yi = sum(y_list)
    sum_xi2 = sum(i**2 for i in x_list)
    sum_yi2 = sum(j**2 for j in y_list)
    sum_xiyi = sum([a * b for a, b in zip(x_list, y_list)])
    l_xx = sum_xi - sum_xi2**2/len(x_list)
    l_yy = sum_yi - sum_yi2**2/len(y_list)
    l_xy = sum_xi - sum_xi*sum_yi/len(x_list)
    b = l_xy / l_xx
    a = sum_yi/len(y_list) - b*sum_xi/len(x_list)
    # 计算相关系数
    rate_r = l_xy / pow(l_xx*l_yy, 2)
    return b,a,rate_r

主函数及运行结果

1
2
3
4
5
6
7
8
9


def main():
    filename = "索引实验数据.csv"
    labmain(filename)
    plot_func(filename)
    b, a , r = reg_func(filename)
    print(f"线性回归方程为 y= {b:.4f}x + {a:.4f} 相关系数r = {r:.4f}")

if __name__ == "__main__":
    main()

生成的图如下：

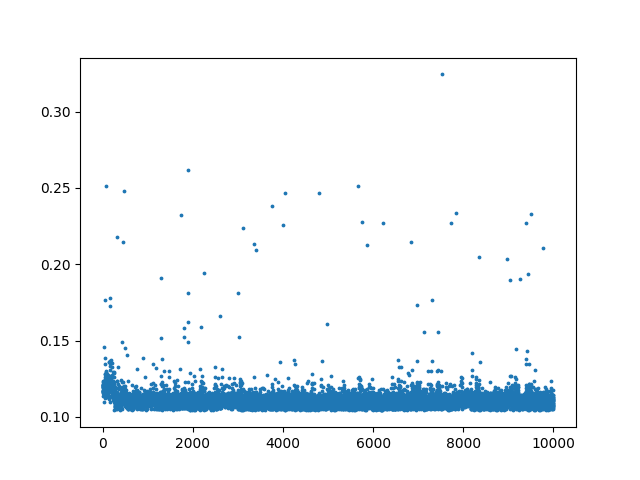
y-n散点图

可以看到，随着 $n$ 增大，运行时间 $y$ 均在某个常数附近，只有极少数点偏离了常数。

控制台输出：

控制台输出

拟合的回归方程为：

$$ \begin{aligned} \widehat{y} &= -0.0000x+0.1129 \\ r &=0.0000 \end{aligned} $$

可以看到 $x$ 的系数为 $0$ ，且相关系数也为 $0$ ，证明 $y$ 与 $x$ 的函数为常数函数。

实验结论

通过对实验数据的分析，证明了Python索引操作的时间复杂度为常数阶。