辗转相除法

最大公因数问题

任给两个不全为零的整数，必存在一个的数，它同时是两个数的因子，这个数称为公因数。

不互质的两个数的公因数可以有多个，寻找最大的公因数就被称为最大公因数问题。

设有两个非零整数$a,b$，其最大公因数可表示为

$$ (a,b) $$

例如，

$$ (4,6) = 2 $$

短除法

小学二年级时我们已经知道，可以使用短除法来先找出所有的较小公因数，再把他们相乘。

例如求$(12,16)$，

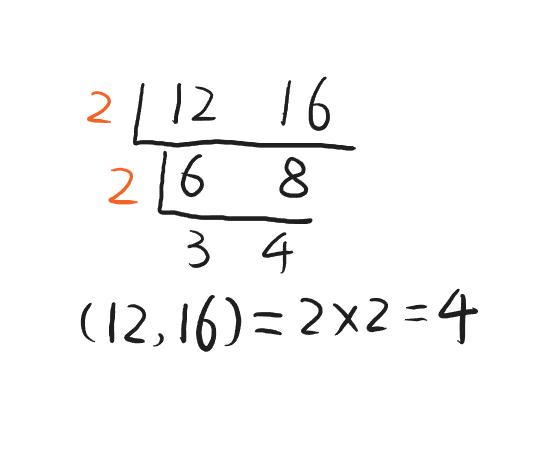
alt text

对于较小的整数，这个方法也蛮好用的，但对于稍大的数，我们很难看出除数是几。比如$(5423,3157)$，使用短除法，找第一个除数都要花不少时间。

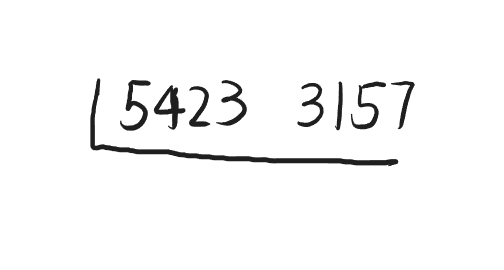
alt text

不难看出，短除法的思路是不断将两个数同时倍比缩小，直到无法继续同除一个数，在这个过程中也就找到了这个最大公因数的因式。但关键在于无法确定每一步的除数，实际情况可能是一个一个试，保险起见还可能是从小到大试。这样的复杂度无异于直接将两数都分解，但我们只需要最大公因数，而我们却多此一举，找出了这个数的因式。

依据这个算法，可以写成

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


def gcd_short_division(a, b):
    if a < b:
        a, b = b, a  # 确保 a 是较大的数

    divisor = 2  # 从最小的质数开始
    gcd = 1      # 初始最大公约数为 1

    while a >= divisor and b >= divisor:
        if a % divisor == 0 and b % divisor == 0:
            # 如果 divisor 是 a 和 b 的公因数
            gcd *= divisor
            a //= divisor
            b //= divisor
        elif a % divisor == 0:
            a //= divisor  # 只对 a 进行除法
        elif b % divisor == 0:
            b //= divisor  # 只对 b 进行除法
        else:
            divisor += 1  # 尝试下一个更大的因数

    return gcd

辗转相除法

定理：设整数$a/b$的余数为$r$,则

$$(a,b)=(b,r)$$

通过不断重复，直到$b_i/r_i=c$可以整除，那么$(a,b)=r_i$

以$(5423,3157)$为例，

alt text

最后$22/11=2$，最后的除数$11$就是最大公因数。

代码实现

该算法是循环过程，当$a>b$时，运算r_1=a%b ，重复r_i=b_(i-1)%r_(i-1)，直到r_i=0，输出r_(i-1)。

代码实现如下，

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


def gcd_euclidean(a, b):
    while b != 0:
        a, b = b, a % b
    return a
# 测试
a = 3157
b = 5423

gcd = gcd_euclidean(a,b)
print(gcd)

注意到，这里不用判断$a,b$的大小,如果 $a<b$，第一次相除后变成了gcd(b,a)

对比短除法，可谓是相当简洁了。

最小公倍数问题

求一个两个数的最小公倍数$(GCD)$，可以用

$$ \begin{aligned} lcm(a,b) = \frac{|a \times b|}{gcd(a,b)} \end{aligned} $$

已知最大公因数，即可求出最小公倍数

代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


def lcm_euclidean(a,b):
    c = a
    d = b
    while d != 0:

        c, d = d, c % d
    lcm = abs(a*b)/c
    return lcm

# 测试
a = 24
b = 28
lcm = lcm_euclidean(a,b)
print(lcm)