初识LaTex数学公式
我们已经知道,计算机能够显示文字,大致要经历下面的过程:将文字 编码 ,利于计算机的识别与存储;显示文字时 解码 ,依据编码系统将文字进行翻译;最后是 渲染,将文字以可见的形式显示,通常是显示文字对应的矢量图。
对于每一个文字,可以设计好一套编解码系统,对应编码设计对应的文字矢量图。这样就可以实现 文字 -> 编码 -> 矢量图 的 映射。
那么,复杂的数学公式是否可以像文字一样简单地表示呢?
在概率论中,正太分布的分布函数为:
$$ F(x) = \frac{1}{\sqrt{2 \pi} \sigma} \int_{- \infty}^{x} e^{-\frac{(x- \mu)^2}{2 \sigma^2}} dx. $$这是一个相当复杂的公式:包含了分数、根号、指数、积分符号和特殊常数(圆周率和自然对数底)。
用 LaTex 可以很简单地表示:
|
|
LaTex 本质上与 HTML 一样,都是 标记语言,用于代码化地组织和构建文本、图像等 元素,并将 元素 可视化。在数学公式方面, LaTex 几乎是所有前端的首选项。
LaTex数学公式
在LaTex中,数学公式要包含在 $$,\[ \]等声明符号内,表明内部是数学公式的代码。最常见的是使用 $ $。
如表示刚才的正太分布函数,可以写成:
|
|
LaTex数学公式是有着一定的结构的。{ } 内的代码将会是一个整体,^{ } 表示上标,_{ } 表示下标。当一个元素既有上标又要下标时,先写下标再写上标。
如表示一个全排列数:
$$ A_5^3 $$
|
|
其他常用的标志符:
-
分式
\frac{分子}{分母} -
四则运算
加法:
+减法:
-乘法:
\times除法:
\div -
微积分
极限:
$$ \lim $$\lim求导:
$$ f^{\prime} $$f^{\prime}积分:
$$ \int $$\int累加:
$$ \sum $$\sum -
矩阵
表示中括号矩阵:
$$ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} $$1 2 3 4 5 6$$ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} $$表示大括号矩阵:
$$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} $$1 2 3 4 5 6$$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} $$表示行列式:
$$ \begin{vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{vmatrix} $$1 2 3 4\begin{vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{vmatrix}这其实不是一个行列式,但仍然可以被“正确”地表示。LaTex只关注公式的形式,而非真正的数学意义。
LaTex的练习环境
CTex
CTex 是LeTex的中国版,提供完整的 LaTex 环境和针对中文的调教。
官网:CTex官网
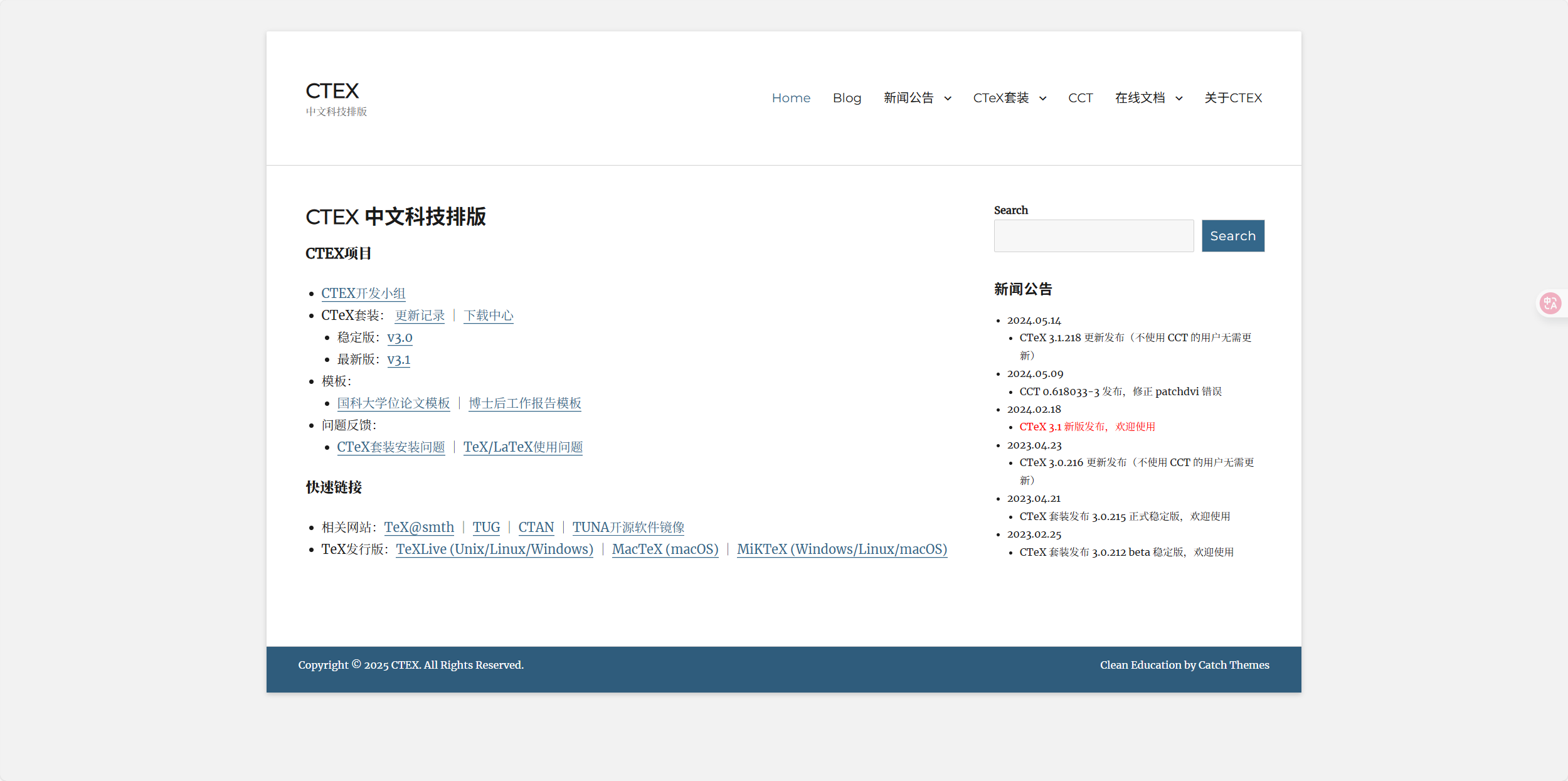
WPS
从2025年开始,WPS新增了LaTex公式的支持。在文档里点击插入 -> 公式 -> 插入LaTex公式
KaTex.js
如果你懂前端,可以将KaTex.js包导入到网站中,在网页中使用数学公式,例如本站就是。
js包官网:KeTex.js
小测
请用 LaTex 格式书写下面题目的解题过程(很简单):
1
(微积分)求定积分:
$$ \int_0^1 \frac{1}{(x+1)(x^2-2x+2)}dx. $$2
(物理)$10g$ 氢气吸收 $1000J$ 的热量时,压强未发生改变,它原来的温度是 $300K$ ,最后的温度是多少?
3
(概率论)一个群体中有一下个体:
-
$k$个纯合显性个体(AA)
-
$m$个杂合子个体(Aa)
-
$n$个纯合隐性个体(aa)
要求:计算随机选取两个个体交配时,后代携带至少一个显性等位基因(即表现为显性性状)的概率。假设任意两个个体均可交配。